recursion multi function call

fibonacci sum

	f(0)->0
	f(1)->1
	f(2)-> f(1)+f(0)
	f(3)-> f(2)+f(1)
	f(4) -> f(4-1)+f(4-2)
	f(n)->f(n-1)+f(n-2)

Print all subsequence

|3|1|2

sub sequence can be created with take and do not take decisions

choose

```fun(int i, []){
	if(i>=n){
		print([])
		return;
	}
	[].add([i])
	fun(i+1, []) // take
	[].remove([i])
	fun(i+1, []) // do not take
}

“

Print subsequence where sum is K

fun(int i, result[], int k){
	int sum = sunFun(result);
	if(i>=result.length || sum>k){
		return;
	}else if(sum==k){
		print(result);
		return;
	}
	result.add(arr[i]);
	fun(i+1, result[],k));
	result.remove(arr[i]);
	fun(i+1, result[], k)
}
Correct solution

fun(int i, result[], int k){
	int sum = sunFun(result);
	if(i==arr.length && sum==k){
		print(result);
		return;
	}
	result.add(arr[i]);
	fun(i+1, result[],k));
	result.remove(arr[i]);
	fun(i+1, result[], k)
}

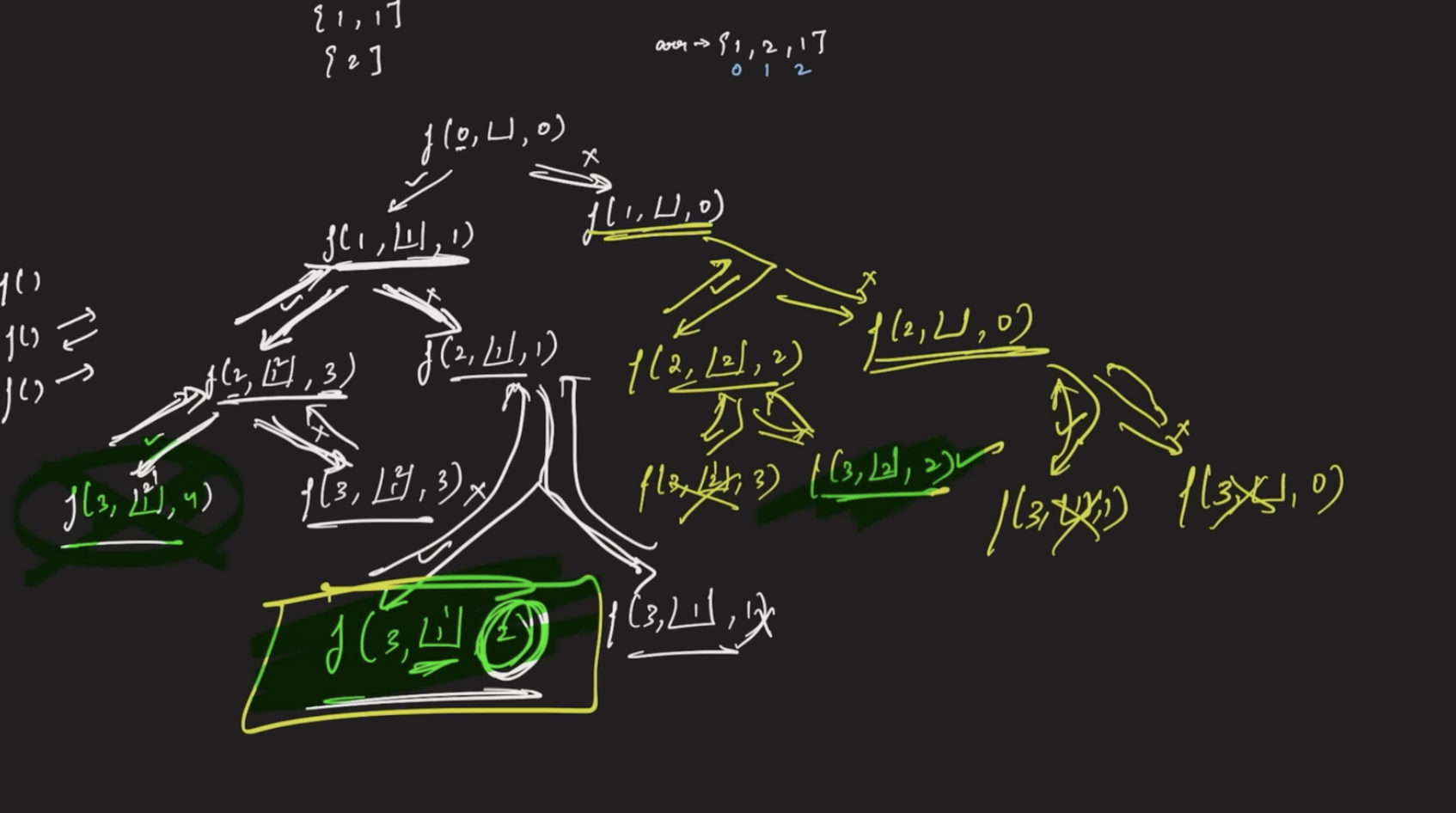
Print any 1 sub sequence

fun(int i, result[], int k){
	int sum = sunFun(result);
	if(i==arr.length && sum==k){
		print(result);
		return true;
	}
	result.add(arr[i]);
	boolean res = fun(i+1, result[],k));
	
	if(!res){
	result.remove(arr[i]);
	res = fun(i+1, result[], k)
	}
	return res
	
}

Print number of subsequence

fun(int i, int sum, int k){
	if(i==arr.length && sum==k){
		return 1;
	}
	else if(i==arr.length ){
		return 0;
	}
	result.add(arr[i]);
	int l= fun(i+1, result[],k))
	
	int r =  = fun(i+1, result[], k)
	
	return l + r;
	
}